Giving Math Cultural Meaning

The journey toward equity in mathematics is not just an enrollment numbers game, as Hammond so eloquently states. Creating equity and leveling the playing field so that students experience mathematics in meaningful ways starts with lessons that are aligned to state standards, have embedded strategies that are purposefully used throughout the lesson cycle to challenge and engage students at high levels, and gather informative feedback to assess learning in real time so that immediate corrections can be made. After all, what use is an exit ticket if there is no time planned to analyze the data collected and make instructional shifts based on it? In mathematics, practice makes permanent.

Equitable practices include multiple components, but this article focuses on planning. Planning sessions often concentrate on curating educational activities from various resources and media, but planning must go beyond curation to include opportunities for all students to develop and advance their metacognition and communication skills. There are two critical, yet practical, components to lesson planning that are often overlooked or underutilized.

1. Language Elements

Planning should include a thorough analysis of the language elements required of each content standard. What I’ll call “academic” language refers to the cognitive verbs typically found in the question stems of assessments and standards. If informally asked questions are overused in daily instruction and questioning, lessons can hinder students’ comprehension of the task at hand.

The use of familiar, informal language is common and seen by some as a way to make mathematics easier to understand. For example, a teacher might ask, “Does this make sense?” But on the assessment, the same question is phrased, “Which of the following is a valid conclusion?,” putting students with limited vocabularies at a great disadvantage. Analyzing word choice can help teachers formulate better questions in the moment and in planning.

To further promote equity, a question can be asked with formal wording, repeated informally, and asked again formally. This helps students learn new vocabulary as they learn math concepts. Additionally, I recommend the use of sentence frames and stems (Figure 1) to give students an opportunity to use the words in their responses. Through this type of analysis, teachers not only plan strategies for language development but also subsequently have an opportunity to understand the standards at a deeper level.

Figure 1: Sentence stems give students the opportunity to rephrase math problems.

Figure 2: A teacher created a classroom activity in which students helped find examples and synonymous terms.

Instructors can then identify specific language elements in designing interactive word walls that address content and graphic or symbolic language elements. Lesson planning should also extend to the design of question sessions that intentionally use and assess each of the language elements through written and oral responses to increase learner engagement.

Figure 2 shows how a teacher took knowledge from a planning session to create a classroom activity that helps students build math vocabulary, supporting their understanding of the standards and preparing them to better create oral and written responses to assessment questions. Short, frequent bursts of speaking and writing about math builds the foundation students need for open-ended tasks that require written justification, and if students aren’t given opportunities to speak about their thinking, they will be ill-equipped to write about it.

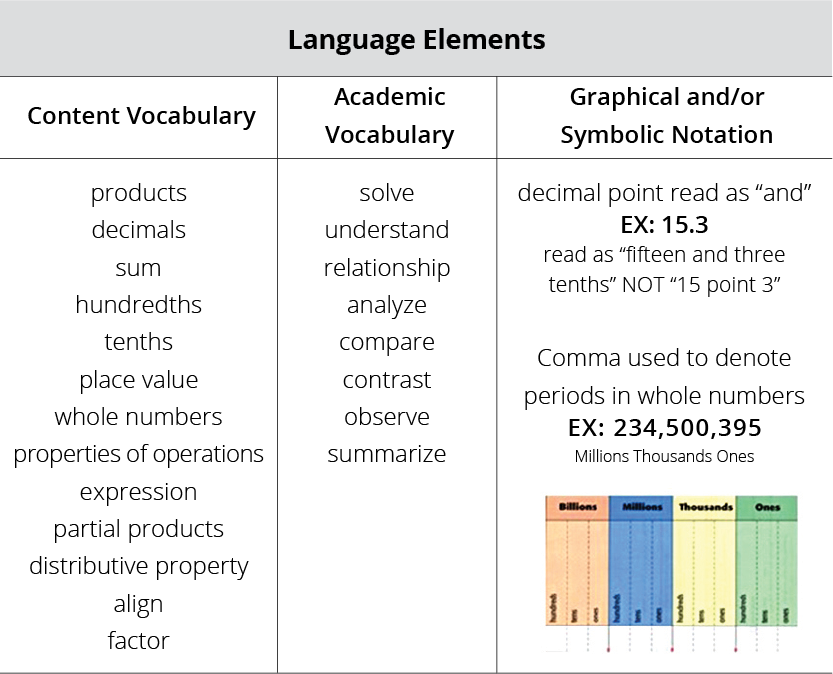
Figure 3: Departmental planning or curriculum writing can include a breakdown of math standards language.

2. Formative Assessments

Every teacher should be able to answer the following question at the end of class: “What percentage of my students ‘got it’?” Lesson planning should allow for an intentional, systematic process to be in place before, during, and after instruction to provide the immediate feedback needed to adjust instruction and improve student achievement. Good formative assessment strategies make data collection throughout the lesson cycle possible and give educators insights into students’ thinking beyond rote memorization and regurgitation.

Figure 4: A list of non-negotiable math vocabulary reminds students how to talk about math.

Formative assessment before the lesson allows the teacher to identify reteaching opportunities and create differentiation before students get the time to rehearse misinformation that’s difficult to unlearn. You can identify small groups for more personal instruction using technology; self-paced, individualized tasks; and co-teacher support. Formative assessment at the beginning of a unit allows students who have achieved mastery to be given tasks more closely aligned with their ability, challenging them in meaningful ways to deter boredom.

Here are a few easy-to-implement formative assessment techniques for the beginning of class:

1. Entry tickets that use the KWL model. Once the learning goal of the day is discussed, students jot down what they already Know about the topic, what they might not understand and Want to know, and what they Learned previously. The exercise promotes a growth mindset in real time to give students the confidence to persevere.
2. Emoji scale reflection. This simple assessment asks students to shade in the emoji that best matches their understanding. They also have to justify their choice by writing an “I can” statement of what they can do or what they need to work on. This strategy also works well during the lesson, if the lesson plan includes a time for reflection in whole-class or small-group discussions.
3. Technology-based assessments. Apps such as Kahoot! and Quizlet are great, but they might not give an accurate assessment due to their multiple-choice nature. Adding group discussion to determine the correct answer once the data is given to students is a great way to push them toward analysis and evaluation. Asking students to use notes and resources to justify their conclusions helps them revise their thinking and deepen understanding.

Offer reflection and discussion opportunities during the teaching of a lesson. There are bound to be roadblocks to mathematical understanding in place—common error patterns, misconceptions, and generalizations associated with the content standards addressed. Again, you don’t want students to rehearse misinformation. Tweak the “Think-Pair-Share” strategy to provide data and offer oral and written communication tasks to target analysis of these roadblocks:

1. Think-Write-Talk-Revise. Consider the “I do, we do, you do” cycle. The teacher has provided examples and highlighted associated error patterns, misconceptions, and overgeneralizations. Before moving to the “we do,” the teacher poses a statement or worked problem for students to analyze and agree or disagree with. After appropriate think time, the teacher provides a sentence frame or stem to jump-start the writing, and students move into a brief discussion with a partner or two. Once they have had a chance to present their thinking, the students can revise their original ideas. Often, a pair-share strategy lacks accountability and might be abandoned because it doesn’t yield the level of discussion desired. By including written reflection, however, teachers can tap into evidence of students’ thinking and assess it. After sharing, revision provides another assessment opportunity and moves students toward a growth mindset goal of learning from their mistakes.
2. Think-Talk-Write. This strategy works well when working with reluctant writers in math, since it provides time to collect thoughts and share ideas prior to writing them down. Students who need to build vocabulary, including emerging bilingual students, can also benefit from using a word bank provided by the teacher that targets content vocabulary for the discussion (see Figure 4).

After instruction is the phase of the lesson on which most assessment concentrates. It’s a necessary phase, but many opportunities might be missed if the end of the lesson gets most or all of the assessment attention. The tried-and-true exit ticket, error analysis, and sticky notes can provide meaningful data, but without “before” and “during” assessments, many students will still struggle with unanswered questions and feelings of doubt.

Analysis of standards and planning for continuous assessment are essential to achieving equity in mathematics instruction, but they by no means represent a comprehensive approach. Building relationships with students, making math relevant to students’ lives, and more strategies are needed. Look for two more installments of this three-part series in future issues of Principal magazine, in which the Benjamin Banneker Association will share additional ideas on advancing equity.

Beatrice Moore Luchin is executive director of Benjamin Banneker Association Inc. and the author of multiple mathematics textbooks and articles focusing on mathematics teaching and learning with an emphasis on equity.

This is the first article in a series about culturally responsive math instruction, contributed by the Benjamin Banneker Association Inc. The next installment will cover aligning your school’s math mission and professional learning goals to advance equity.